Introduction
The previous chapter explained how Feed-forward Neural Networks (FNNs) can be used for multi-class classification of 28 x 28 pixel handwritten digits from the MNIST dataset. While FNNs work well for this type of task, they have significant limitations when dealing with larger, high-resolution color images.
In neural network terminology, each RGB value of an image is treated as an input feature. For instance, a high-resolution 600 dpi RGB color image with dimensions 3.937 x 3.937 inches contains approximately 5.58 million pixels, resulting in roughly 17 million RGB values.
If we use a fully connected FNN for training, all these 17 million input values are fed into every neuron in the first hidden layer. Each neuron must compute a weighted sum based on these 17 million inputs. The memory required for storing the weights depends on the numerical precision format used. For example, using the 16-bit floating-point (FP16) format, each weight requires 2 bytes. Thus, the memory requirement per neuron would be approximately 32 MB. If the first hidden layer has 10,000 neurons, the total memory required for storing the weights in this layer would be around 316 GB.
In contrast, Convolutional Neural Networks (CNNs) use shared weight matrices called kernels (or filters) across all neurons within a convolutional layer. For example, if we use a 3x3 kernel, there are only 9 weights per color channel. This reduces memory usage and computational costs significantly during both the forward and backward passes.
Another limitation of FNNs for image recognition is that they treat each pixel as an independent unit. As a result, FNNs do not capture the spatial relationships between pixels, making them unable to recognize the same object if it shifts within the frame. Additionally, FNNs cannot detect edges or other important features. On the other hand, CNNs have a property called translation invariance, which allows the model to recognize patterns even if they are slightly shifted (small translations along the x and y axes). This helps CNNs classify objects more accurately. Furthermore, CNNs are more robust to minor rotations or scale changes, though they may still require data augmentation or specialized network architectures to handle more complex transformations.
Convolution Layer
Convolution Process
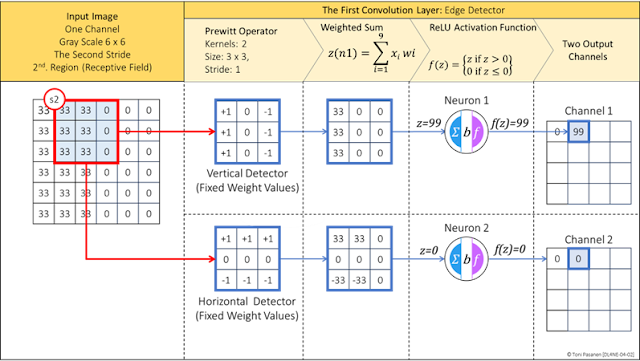
The purpose of the convolution process is to extract features from the image and reduce the number of input parameters before passing them through fully-connected layers. The convolution operation uses a shared weight matrix called kernels or filters, which are shared across all neurons within a convolutional layer. In this example, we use the Prewitt operator, which consists of two 3x3 kernels with fixed weight values for detecting vertical and horizontal edges.
In the first step, these two kernels are positioned over the first region of the input image, and each pixel value is multiplied by the corresponding kernel weight. Next, the process computes the weighted sum, z=0, and the result is passed through the ReLU activation function. The resulting activation values, f(z)=0 , contribute to the neuron-based output channels.
Since our input image is a grayscale image without color channels (unlike an RGB image), it has only one input channel. By using two kernels, we obtain two output channels: one for detecting vertical edges and the other for detecting horizontal edges. The formula for calculating the size of the output channel:
Height
= (Image h – Kernel h)/Stride + bias = (6-3)/1
+ 1 = 4
Width =
(Image w – Kernel w)/Stride + bias = (6-3)/1 + 1 = 4
Figure 4-1: Convolution Layer – Stride One.
After calculating the first value for the output channel using the image values in the first region, the kernel is shifted one step to the right (stride of 1) to cover the next region. The convolution process calculates the weighted sum based on the values in this region and the weights of the kernel. The result is then passed through the ReLU activation function. The output of the ReLU activation function differs: for the first output channel, it is f(z)=99; for the second output channel, it is f(z)=0. Figure 4-3 depicts the fifth stride.
Figure 4-2: Convolution Layer – Stride Two.
Figure 4-3: Convolution Layer – Stride Five.
The sixteenth stride, shown in Figure 4-4, is the last one. Now output channels one and two are filled.
Figure 4-4: Convolution Layer – Stride Sixteenth.
Figure 4-5 shows how the convolution process found one vertical edge and zero horizontal edge from the input image. The convolution process produces two output channels, each with a size of 4 × 4 pixels, while the original input image was 6 × 6 pixels.
Figure 4-5: Convolution Layer – Detected Edges.
MaxPooling
MaxPooling is used to reduce the size of the output channels if needed. In our example, where the channel size is relatively small (4 × 4), MaxPooling is unnecessary, but we use it here to demonstrate the process. Similar to convolution, MaxPooling uses a kernel and a stride. However, instead of fixed weights associated with the kernel, MaxPooling selects the highest value from each covered region. This means there is no computation involved in creating the new matrix. MaxPooling can be considered as a layer or part of the convolution layer. Due to its non-computational nature, I see it as part of the convolution layer rather than a separate layer.
Figure 4-6: Convolution Layer: MaxPooling.
The First Convolution Layer: Convolution
In this section, we take a slightly different view of convolutional neural networks compared to the preceding sections. In this example, we use the Kirsch operator in the first convolution layer. It uses 8 kernels for detecting vertical, horizontal, and diagonal edges. Similar to the Prewitt operator, the Kirsch operator uses fixed weight values in its kernels. These values are shown in Figure 4-7.
Figure 4-8: Kirsch Operator.
In Figure 4-8, we use a pre-labeled 96 x 96 RGB image for training. An RGB image has three color channels: red, green, and blue for each pixel. It is possible to apply all kernels to each color channel individually, resulting in 3 x 8 = 24 output channels. However, we follow the common practice of applying the kernels to all input channels simultaneously, meaning the eight Kirsch kernels have a depth of 3 (matching the RGB channels). Each kernel processes the RGB values together and produces one output channel. Thus, each neuron uses 3 (width) x 3 (height) x 3 (depth) = 27 weight parameters for calculating the weighted sum. With a stride value of one, the convolution process generates eight 94 x 94 output channels. The formula for calculating weighted sum:
Figure 4-8: The First Convolution Layer – Convolution Process.
The First Convolution Layer: MaxPooling
To reduce the size of the output channels from the first convolution layer, we use MaxPooling. We apply eight 2 x 2 kernels, each with a depth of 8, corresponding to the output channels. All kernels process the channels simultaneously, selecting the highest value among the eight channels. MaxPooling with this setting reduces the size of each output channel by half, resulting in eight 47 x 47 output channels, which are then used as input channels for the second convolution layer
Figure 4-9: The First Convolution Layer – MaxPooling.
The Second Convolution Layer
Figure 4-10 shows both the convolution and MaxPooling processes. The eight 47 x 47 output channels produced by the first convolution layer are used as input channels for the second convolution layer. In this layer, we use 16 kernels whose initial weight values are randomly selected and adjusted during the training process. The kernel size is set to 3 x 3, and the depth is 8, corresponding to the number of input channels. Thus, each kernel calculates a weighted sum over 3 x 3 x 8 = 72 parameters with 72 weight values. All 16 kernels produce new 45 x 45 output channels by applying the ReLU activation function. Before flattening the output channels, our model applies a MaxPooling operation, which selects the highest value within the kernel coverage area (region). This reduces the size of the output channels by half, from 45 x 45 to 22 x 22.
If we had used the original image without convolutional processing as input to the fully connected layer, there would have been 27,648 input parameters (96 x 96 x 3). Thus, the two convolution layers reduce the number of input parameters to 7,744 (22 x 22 x 16), which is approximately a 72% reduction.
Figure 4-10: The Second Convolution Layer – Convolution and MaxPooling.
Fully Connected Layers
Before feeding the data into the fully connected layer, the multi-dimensional 3D array (3D tensor) is converted into a 1D vector. This produces 7,744 input values (22 x 22 x 16) for the input layer. We use 4,000 neurons with the ReLU activation function in the first hidden layer, which is approximately half the number of input values. In the second hidden layer, we have 1,000 neurons with the ReLU function. The last layer, the output layer, has 10 neurons using the SoftMax function.
Figure 4-11: Fully Connected Layer – Convolution and MaxPooling.
Backpropagation Process
In Fully Connected Neural Networks (FCNNs), every neuron has its own unique set of weights. In contrast, Convolutional Neural Networks (CNNs) use parameter sharing, where the same filter (kernel) is applied across the entire input image. This approach not only reduces the number of parameters but also enhances efficiency.
Additionally, backpropagation in CNNs preserves the spatial structure *) of the input data through convolution and pooling operations. This helps the network learn spatial features like edges, textures, and patterns. In contrast, FCNNs flatten the input data into a 1D vector, losing any spatial information and making it harder to capture meaningful patterns in images.
*) Spatial features refer to the characteristics of an image that describe the relationship between pixels based on their positions. These features capture the spatial structure of the image, such as edges, corners, textures, shapes, and patterns, which are essential for recognizing objects and understanding the visual content.