Introduction of an Artificial Neuron

 Introduction 

Before diving into the somewhat complex world of Artificial Intelligence (AI), let’s first consider what intelligence means from a human perspective. Judo, as a martial art, serves as a good—though not an obvious—example. I trained in judo for over 20 years. During that time, I learned which throwing techniques to use to take down an opponent efficiently by leveraging their movement energy and reactions. But how did I learn that? Through a supervised training process, where our coach first taught us the throwing techniques and the situations in which they work best. Then, we practiced them ourselves. Mastering these techniques requires thousands of repetitions before achieving perfection. Ultimately, timing and reaction to the opponent’s movements play a significant role in determining whether a throw is successful or not. After mastering several throwing technics, I was capable of apply them in the situation not necessarily to seen before.

How does this relate to Artificial Intelligence (AI)? AI is a broad term encompassing solutions that aim to mimic human brain functions. A subset of AI is Machine Learning (ML), which enables systems to make decisions based on input data without being explicitly programmed for each scenario. The driving force behind this capability is Deep Learning (DL), which utilizes Deep Neural Networks (DNNs). The intelligence of these networks resides in thousands of neurons (Perceptron) and their interconnections which together form a neural network.

Training a Neural Network to perform well in its given task follows the same principles as training a human to execute a perfectly timed and well-performed throwing technique, for example. The training process takes time, requires thousands of iterations, and involves analyzing results before achieving the expected, high-quality outcome.When training Neural Networks, we use a training dataset that, in addition to input data, includes information about the expected output (supervised learning). Before deploying the network into production, it is tested with a separate test dataset to evaluate how well it performs on unseen data.

The duration of the training process depends on several factors, such as dataset size, network architecture, hardware, and selected parallelization strategies (if any). Training a neural network requires multiple iterations—sometimes even tens of thousands—where, at the end of each iteration, the model's output is compared to the actual value. If the difference between these two values is not small enough, the network is adjusted to improve performance. The entire process may take months, but the result is a system that responds accurately and quickly, providing an excellent user experience.

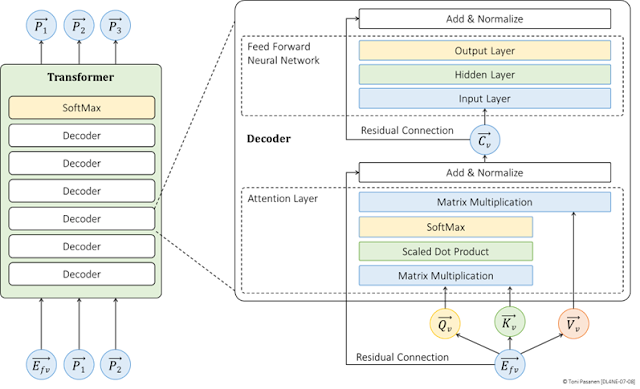
This chapter begins by discussing the artificial neuron, and its functionality. We then move on to the Feedforward Neural Network (FFNN) model, first explaining its layered structure and how input data flows through it in a process called the Forward Pass (FP). Next, we examine how the FFNN is adjusted during the Backward Pass (BP), which fine-tunes the model by minimizing errors. The combination of FP and BP is known as the Backpropagation Algorithm.

Artificial Neuron 

An artificial neuron, also known as a perceptron, is a fundamental building block of any neural network. It functions as a computational unit that processes input data in two phases. First, it collects and processes all inputs, and then applies an activation function. Figure 1-1 illustrates the basic process without the complex mathematical functions (which I will explain later for those interested in studying them). On the left-hand side, we have a bias term and two input values, x1 and x2. The bias and inputs are connected to the perceptron through adjustable weight parameters: w0, w1, and w2, respectively. During the initial training phase, weight values are randomly generated.

Weighted Sum and Activation Function

As the first step, the neuron calculates the weighted sum of inputs x1 and x2 and adds the bias. A weighted sum simply means that each input is multiplied by its corresponding weight parameter, the results are summed, and the bias is added to the total. The bias value is set to one, so its contribution is always equal to the value of its weight parameter. I will explain the purpose of the bias term later in this chapter. The result of the weighted sum is denoted as z, which serves as a pre-activation value. This value is then passed through a non-linear activation function, which produces the actual output of the neuron, y ̂ (y-hat). Before explaining what non-linearity means in the context of activation functions and why it is used, consider the following: The input values fed into a neuron can be any number between negative infinity (-∞) and positive infinity (+∞). Additionally, there may be thousands of input values. As a result, the weighted sum can become a very large positive or negative value.

Now, think about neural networks with thousands of neurons. In Feedforward Neural Networks (FFNNs), neurons are structured into layers: an input layer, one or more hidden layers, and an output layer. If input values were only processed through the weighted sum computation and passed to the next layer, the neuron outputs would grow linearly with each layer. Even if we applied a linear activation function, the same issue would persist—the output would continuously increase. With a vast number of neurons and large input values, this uncontrolled growth could lead to excessive computational demands, slowing down the training process. Non-linear activation functions help keep output values within a manageable range. For example, an S-shaped Sigmoid activation function squeezes the neuron’s output to a range between 0 and 1, even for very large input values.

Let’s go back to Figure 1-1, where we first multiply the input values by their respective weight parameters, sum them, and then add the bias. Since the bias value is 1, it is reasonable to represent it using only its associated weight parameter in the formula. If we plot the result z on the horizontal axis of a two-dimensional chart and draw a vertical line upwards, we obtain the neuron’s output value y at the point where the line intersects the S-curve. Simple as that. Naturally, there is a mathematical definition and equation for this process, which is depicted in Figure 1-2. 

Before moving on, there is one more thing to note. In the figure below, each weight has an associated adjustment knob. These knobs are simply a visual representation to indicate that weight values are adjustable parameters, which will be tuned by the backpropagation algorithm in case the model output is not close enough to expected result. The backpropagation process is covered in detail in a dedicated chapter.

Figure 1-1: An Architecture of an Artificial Neuron.

Figure 1-2 shows the mathematical equations for calculating the weighted sum and the Sigmoid function. The Greek letter used in the weighted sum equation is Σ (uppercase Sigma). The lowercase i is set to 1 beneath the Sigma symbol, indicating that the weighted sum calculation starts from the first pair of elements: input x1 and its corresponding weight w1. The notation n=2 specifies the total number of paired elements included in the weighted sum calculation. In our example, both input values and their respective weights are included.

After computing the weighted sum, we add the bias term. The result, z, is then passed through the Sigmoid function, producing the output y ̂. The Sigmoid function is commonly represented by the Greek letter σ (lowercase sigma).

The lower equation in Figure 1-2 shows how the Sigmoid function is computed. To obtain the denominator for the fraction, Euler’s number (e≈2.71828) is raised to the power of −z and then summed with 1. The final output is simply the reciprocal of this sum.

Figure 1-2: The Math Behind an Artificial Neuron.

The formulas can be expressed in an even simpler manner using dot products, which are commonly used in linear algebra. Dot products frequently appear in research papers and deep learning literature.

In Figure 1-3, both input values and weights are arranged as column vectors. The notation for the input vector uses an uppercase X, while the weight vector is denoted by an uppercase W. Although these are technically vectors, it is not a major issue to illustrate them as a simple matrix for demonstration purposes. Generally speaking, a matrix has more than one row and column, as you will learn later.

The dot product performs a straightforward matrix multiplication, as shown in the figure. This greatly simplifies the computation.

Figure 1-3: Matrix Multiplication with Dot Product.

Bias term

Figures 1-4 and 1-5 illustrate how changes in the bias weight parameter affect the weighted sum and shift z horizontally. This, in turn, changes the output of the Sigmoid function and the neuron’s final output.

In Figure 1-4, the initial weight values for the bias, input x1, and input x2 are +0.3, +0.5, and −0.3, respectively. The calculated weighted sum is z=4.8. Applying the Sigmoid function to output z=4.8, we obtain an output value of 0.992. Figure 1-4 visualizes this process: z=4.8 is positioned on the horizontal axis, and the intersection with the S-curve results in an output of 0.992.

Figure 1-4: Construct of an Artificial Neuron.

Now, we adjust the weight w0 associated with the bias from +0.3 down to −4.0. As a result, the weighted sum decreases from 4.84 to 0.50, shifting z 4.3 steps to the left on the horizontal axis. Applying the Sigmoid function to z, the neuron’s output decreases from 0.992 to 0.622.

Figure 1-5: Construct of an Artificial Neuron.

In the example calculation above, imagine that input values x1 and x2 are zero. Without a bias term, the activation value will be zero, regardless of how large the weight parameters are. Therefore, the bias term also allows the neuron to produce non-zero outputs, even when all input values are zero.

ReLU Activation Function

A lighter alternative to the Sigmoid activation function is ReLU (Rectified Linear Unit). The ReLU activation function is non-linear for values less than or equal to zero and linear for values greater than zero. This means that if the weighted sum z≤0, the output is zero. If z>0, the output is equal to z.

From a computational perspective, ReLU requires fewer CPU cycles than the Sigmoid function. Figure 1-6 illustrates how z=4.8 is processed by ReLU, resulting in an output value of y ̂=4.8. The figure also shows two common notations for ReLU. The first notation states:

• If z>0, return z.
• If z≤0, return 0.

The second notation, written as MAX(0,z), simply means selecting the greater value between 0 and z.

Figure 1-6: Artificial Neuron with a ReLU Activation Function. 

Network Impact

A single artificial neuron is the smallest unit of a neural network. The size of the neuron depends on its connections to input nodes. Every connection has an associated weight parameter, which is typically a 32-bit value. In our example, with 2 connections and bias, the size of the neuron is 3 x 32 bits = 96 bits.

Although we haven’t defined the size of the input in this example, let’s assume that each input (x) is an 8-bit value, giving us 2 x 8 bits = 16 bits for the input data. Thus, our single neuron "model" requires 96 bits for the weights plus 16 bits for the input data, totaling 112 bits of memory. This is small enough to not require parallelization. Besides, the weight parameters and input values, the result of weighted sum and the neuron output must be stored for processing. 

However, if the memory requirement of the neural network model combined with the input data (the "job") exceeds the memory capacity of a GPU, a parallelization strategy is needed. The job can be split across multiple GPUs within a single server, with synchronization happening over high-speed NVLink. If the job must be divided between multiple GPU servers, synchronization occurs over the backend network, which must provide lossless, high-speed packet forwarding.

Parallelization strategies will be discussed in the next chapter, which introduces a Feedforward Neural Network using the Backpropagation algorithm, and in later chapters dedicated to Parallelization.

Summary

Deep Learning leverages Neural Networks, which consist of artificial neurons. An artificial neuron mimics the structure and operation of a biological neuron. Input data is fed to the neuron through connections, each with its own weight parameter. The neuron uses these weights to calculate a weighted sum of the inputs, known as the pre-activation value. This result is then passed through an activation function, which provides the post-activation value, or the actual output of the neuron. The activation functions discussed in this chapter are the non-linear ReLU (Rectified Linear Unit) and logistic Sigmoid functions.

References

Yann LeCun, Corina Cortes, Christoper J.C. Burges: The MNIST database of handwritten digits. 

Alex Krizhevsky, Vinod Nair, and Geoffrey Hinton: The CIFAR-10 dataset

Alex Krizhevsky, Learning Multiple Layers of Features from Tiny Images, April 2009

Jason Brownlee: A Gentle Introduction to the Rectified Linear Unit (ReLU), August 20, 2020.

Eric W. Weisstein: Wolfram Mathworld – Hyperbolic Tangent

Eric W. Weisstein: Wolfram Mathworld – Sigmoid Tangent

Large Language Model (LLM) - Part 2/2: Transformer Architecture

 Introduction

Sequence-to-sequence (seq2seq) language translation and Generative Pretrained Transformer (GPT) models are subcategories of Natural Language Processing (NLP) that utilize the Transformer architecture. Seq2seq models are typically using Long Short-Term Memory (LSTM) networks or encoder-decored based Transformers. In contrast, GPT is an autoregressive language model that uses decoder-only Transformer mechanism. The purpose of this chapter is to provide an overview of the decoder-only Transformer architecture.

The Transformer consists of stacks of decoder modules. A word embedding vector, a result of the word tokenization and embbeding, is fed as input to the first decoder module. After processing, the resulting context vector is passed to the next decodeer, and so on. After the final decoder, a softmax layer evaluates the output against the complete vocabulary to predict the next word. As an autoregressive model, the predicted word vector from the softmax layer is converted into a token before being fed back into the subsequent decoder layer. This process involves a token-to-word vector transformation prior to re-entering the decoder.

Each decoder module consists of an attention layer, Add & Normalization layer and a feedforward neural network (FFNN). Rather than feeding the embedded word vector (i.e., token embedding plus positional encoding) directly into the decoder layers, the Transformer first computes the Query (Q), Key (K), and Value (V) vectors from the word vector. These vectors are then used in the self-attention mechanism. Initially, the query vector is multiplied by the key vectors using matrix multiplication. The result is then divided by the square root of the dimension of the key vectors (scaled dot product) to obtain the logits. The logits are processed by a softmax layer to compute probabilities. The SoftMax prediction results are multiplied with the value vectors to produce a context vector.

Before feeding the context vector into the feedforward neural network, it is summed with the original word embedding vector (which includes positional encoding) via a residual connection. Finally, the output is normalized using layer normalization. This normalized output is then passed as input to the FFNN, which computes the output. 

The basic architecture of the FFNN in the decoder is designed so that the input layer has as many neurons as the dimension of the context vector. The hidden layer, in turn, has four times as many neurons as the input layer, while the output layer has the same number of neurons as the input layer. This design guarantees that the output vector of the FFNN has the same dimension as the context vector. Like the attention block, the FFNN block also employs residual connections and normalization.

Figure 7-8: Decoder-Only Transformer Architecture.

Query, Key and Value Vectors

As pointed out in the Introduction, the word embedding vector is not used as input to the first decoder. Instead, it is multiplied by pretrained Query, Key, and Value weight matrices. The result of this matrix multiplication, dot product, produces the Query, Key, and Value vectors, which are use as inputs, and are processed through the Transformer. Figure 7–9 show the basic workflow of this process.

Figure 7-9: Query, Key, and Value Vectors.

Let’s take a closer look at the process using numbers. After tokenizing the input words and applying positional encoding, we obtain a final 5-dimensional word matrix. To reduce computation cycles, the process reduces the dimension of the Query vector from 5 to 3. Because we want the Query vector to be three-dimensional, we use three 5-dimensional column vectors, each of which is multiplied by the word vector.

Figure 7-10: Calculating the Query Vector.

Figure 7–11 depicts the calculation process, where each component of the word vector is multiplied by its corresponding component in the Query weight matrix. The weighted sum of these results forms a three-dimensional Query vector. The Key and Value vectors are calculated using the same method.

The same Query, Key, and Value (Q, K, V) weight matrices are used across all words (tokens) within a single self-attention layer in a Transformer model. This ensures that each token is processed in the same way, maintaining consistency in the attention computations. However, each decoder layer in the Transformer has its own dedicated Q, K, and V weight matrices, meaning that every layer learns different transformations of the input tokens, allowing deeper layers to capture more abstract representations.

Figure 7-11: Calculating the Query Vector.

Attention Layer

Figure 7-12 depicts what happens in the first three components of the Attention layer after calculating the Query, Key, and Value vectors. In this example, we focus on the word “clear”, and try to predict the next word. Its Query vector is multiplied by its own Key vector as well as by all the Key vectors generated for the preceding words. Each multiplication produces its own score. Note that the score values shown in the figure are theoretical and are not derived from the actual Qv × Kv matrix multiplication; however, the remaining values are based on these calculations. Additionally, in our example, we use one-dimensional values (instead of actual vectors) to keep the figures and calculations simple. In reality, these are n-dimensional vectors.

After the Qv × Kv matrix multiplication, the resulting scores are divided by the square root of the vector depth, yielding logits, i.e., the input values for the softmax function. The softmax function then computes the exponential of each logit (using Euler’s number, approximately 2.71828) and divides each result by the sum of all exponentials. For example, the value 3.16, corresponding to the first word, is divided by 482.22, resulting in a probability of 0.007. Note that the sum of the probabilities is 1.0. Softmax ensures that the attention scores sum to 1, making them interpretable as probabilities and helping the model decide which input tokens to focus on when generating an output. In our example, the token for the word “clear” has the highest probability at this stage. The word “decided” has the second highest probability score (0.210), which indicates that the semantics of “clear”, which has the highest probability score (0.665), can be interpreted as an verb answering the question: “What she decided to do?

Figure 7-12: Attention Layer, the First Three Steps.

Next, the SoftMax probabilities are multiplied by each token's Value vector (matrix multiplication). The resulting vectors are then summed, producing the Context vector for the token associated with the word “clear.” Note that the components of the Value vectors are example values and are not derived from actual computations.

Figure 7-13: Attention Layer, the Fourth Step.

Add & Normalization

As the final step, the Word vector, which includes positional encoding, is added to the context vector via a Residual Connection. The result is then passed through a normalization process, where the vector’s components are summed and divided by the vector’s dimension, yielding the mean (μ). This mean value is then used for standard deviation calculation: the mean is subtracted from each of the three vector components, and the results are squared. These squared values are then summed, divided by three (the vector’s dimension), and the square root of this result gives the final output vector [1.40, -0.55, -0.87] of the Add & Normalize layer. 

Figure 7-14: Add & Normalize Layer – Residual Connection and Layer Normalization.

Feed Forward Neural Network

Within the decoder module, the feedforward neural network uses the output vector from the Add & Normalize layer as its input. In our example, the FFNN have one neuron in input layer for each component of the vector. This layer simply passes the input values to the hidden layer, where each neuron first calculates a weighted sum and then applies the ReLU activation function. In our example, the hidden layer contains nine neurons (three times the number of input neurons). The output from the hidden layer is then fed to the output layer, where the neurons again compute a weighted sum and apply the ReLU activation function. Note that in transformer-based decoders, the FFNN is applied to each token individually. This means that each token-related output from the attention layer is processed separately by the same FFNN model with shared weights, ensuring a consistent transformation of each token's representation regardless of its position in the sequence.

Figure 7-15: Fully Connected Feed Forward Neural Network (FFNN).

The final decoder output is computed in the Add & Normalize layer, similarly as Add & Normalize after the attention layer. This produces the decoder output, which is used as the input for the next decoder module. 

Figure 7-16: Add & Normalize Layer – Residual Connection and Layer Normalization.

Next Word Probability Computation – SoftMax Function

The output of the last decoder module does not directly represent the next word. Instead, it must be transformed into a probability distribution over the entire vocabulary. First, the decoder output is passed through a weight matrix that maps it to a new vector, where each element corresponds to a word in the vocabulary. For example, in Figure 7-17 the vocabulary consists of 12 words. These words are tokenized and linked to their corresponding word embeddings vector. That said, the word embedding matrix serves as a weight matrix.

Figure 7-17: Hidden State Vector and Word Embedding Matrix.

Figure 7-18 illustrates how the decoder output vector (i.e., the hidden state h) is multiplied by all word embedding vectors to produce a new vector of logits. 

Figure 7-18: Logits Calculation – Dot Product of Hidden State and Complete Vocabulary.

Next, the SoftMax function is applied to the logits. This function converts the logits into probabilities by exponentiating each logit and then normalizing by the sum of all exponentiated logits. The result is a probability distribution in which each value represents the likelihood of selecting a particular word as the next token.

Figure 7-19: Probability Calculation - Adding Logits to SoftMax Function

Finally, the word with the highest probability is selected as the next token. This token is then mapped back to its corresponding word using a token-to-word lookup. This initiates the next iteration, where the token is converted into its word embedding vector, and used together with positional encoding to create the actual word embedding for the next iteration.

Figure 7-20: Word-to-Token, and Token-to-Word Embedding Process.

In theory, our simple example shows that the model can assign the highest probability to the correct word. For instance, by analyzing the position of the word “clear” relative to its preceding words, the model is able to infer the context. When the context implies that an action is directed toward a known target, the article “the” receives the highest probability score and is predicted as the next word.

Conclusion

We use pretty simple examples in this chapter. However, GPT-3, for example, is built on a deep Transformer architecture comprising 96 decoder blocks. Each decoder block is divided into three primary sub-layers:

Attention Layer: This layer implements multi-head self-attention using four key weight matrices, one each for the query, key, and value projections, plus one for the output projection. Together, these matrices account for roughly 600 million trainable parameters per block.

Add & Normalize Layers: Each block employs two residual connections paired with layer normalization. The first Add & Normalize operation occurs immediately after the Attention Layer, and the second follows the Feed-Forward Neural Network (FFNN) layer. Although essential for stabilizing training, the parameters in each normalization step are relatively few, typically on the order of tens of thousands.

Feed-Forward Neural Network (FFNN) Layer: The FFNN consists of two linear transformations with an intermediate expansion (usually about four times the model’s hidden size). This layer contributes approximately 1.2 billion parameters per block.

Aggregating the parameters from all 96 decoder blocks, and including additional parameters from the token embeddings, positional encodings, and other components, the entire GPT-3 model totals around 175 billion trainable parameters. This is why parallelism is essential: the training process must be distributed across multiple GPUs and executed according to a selected parallelization strategy. The second part of the book discusses about Parallelization.

Large Language Models (LLM) - Part 1/2: Word Embedding

Introduction

This chapter introduces the basic operations of Transformer-based Large Language Models (LLMs), focusing on fundamental concepts rather than any specific LLM, such as OpenAI’s GPT (Generative Pretrained Transformer).The chapter begins with an introduction to tokenization and word embeddings, which convert input words into a format the model can process. Next, it explains how the transformer component leverages decoder architecture for input processing and prediction. 

This chapter has two main goals. First, it explains how an LLM understands the context of a word. For example, the word “clear” can be used as a verb (Please, clear the table.) or as an adjective (The sky was clear.), depending on the context. Second, it discusses why LLMs require parallelization across hundreds or even thousands of GPUs due to the large model size, massive datasets, and the computational complexity involved.

Tokenizer and Word Embedding Matrix

As a first step, we import a vocabulary into the model. The vocabulary used for training large language models (LLMs) typically consists of a mix of general and domain-specific terms, including basic vocabulary, technical terminology, academic and formal language, idiomatic expressions, cultural references, as well as synonyms and antonyms. Each word and character is stored in a word lookup table and assigned a unique token. This process is called tokenization.

Many LLMs use Byte Pair Encoding (BPE), which splits words into subword units. For example, the word "unhappiness" might be broken down into "un," "happi," and "ness." BPE is widely used because it effectively balances vocabulary size and tokenization efficiency, particularly for handling rare words and sub-words. For simplicity, we use complete words in all our examples.

Figure 7-1 illustrates the relationship between words in the vocabulary and their corresponding tokens. Token values start from 2 because token 0 is reserved for padding and token 1 for unknown words.

Each token, representing a word, is mapped to a Word Embedding Vector, which is initially assigned random values. The collection of these vectors forms a Word Embedding Matrix. The dimensionality of each vector determines how much contextual information it can encode.

For example, consider the word “clear.” A two-dimensional vector may distinguish it as either an adjective or a verb but lacks further contextual information. By increasing the number of dimensions, the model can capture more context and better understand the meaning of the word. In the sentence “The sky was clear,” the phrase “The sky was” suggests that "clear" is an adjective. However, if we extend the sentence to “She decided to clear the backyard of junk,” the word "clear" now functions as a verb. More dimensions allow the model to utilize surrounding words more effectively for next-word prediction. For instance, GPT-3 uses 12,288-dimensional vectors. Given a vocabulary size of 50,000 words used by GPT-3, the Word Embedding Matrix has dimensions of 12,288 × 50,000, resulting in 614,400,000 parameters.

The context size, defined as the sequence length of vectors, determines how many preceding words the model considers when predicting the next word. In GPT-3, the context size is 2,048 tokens.

Figure 7-1: Tokenization and Word Embedding Matrix.

 

Word Embedding

As a first step, when we feed input words into a Natural Language Processing (NLP) model, we must convert them into a format the model can understand. This is a two-step process:

1. Tokenization – Each word is assigned a corresponding token from a lookup table.
2. Word Embedding – These token IDs are then mapped to vectors using a word embedding lookup table.

To keep things simple, Figure 7-2 uses two-dimensional vectors in the embedding matrix. Instead of complete sentences, we use words, which can be categorized into four groups: female, male, adult, and child.

The first word, "Wife," appears in the lookup table with the token value 2. The corresponding word vector in the lookup table for token 2 is [-4.5, -3.0]. Note that Figure 7-2 represents vectors as column vectors, whereas in the text, I use row vectors—but they contain the same values.

The second word, "Mother," is assigned the token 3, which is associated with the word vector [-2.5, +3.0], and so on.

Figure 7-2: Word Tokenization and Word Embedding.

In Figure 7-3, we have a two-dimensional vector space divided into four quadrants, representing gender (male/female) and age (child/adult). Tokenized words are mapped into this space.

At the start of the first iteration, all words are placed randomly within the two-dimensional space. During training, our goal is to adjust the word vector values so that adults are positioned on the positive side of the Y-axis and children on the negative side. Similarly, males are placed in the negative space of the X-axis, while females are positioned on the positive side.

Figure 7-3: Words in the 2 Dimensional Vector Space in the Initial State.

Figure 7-4 illustrates how words may be positioned after successful training. All words representing a male adult are placed in the upper-left quadrant (adult/male). Similarly, all other words are positioned in the two-dimensional vector space based on their corresponding age and gender.

Figure 7-4: Words in the 2 Dimensional Vector Space After Training.

In addition to grouping similar words, such as "adult/female," close to each other in an n-dimensional space, there should also be positional similarities between words in different quadrants. For example, if we calculate the Euclidean distance between the words Father and Mother, we might find that their distance is approximately 4.3. The same pattern applies to word pairs like Nephew-Niece, Brother-Sister, Husband-Wife, and Father-in-Law–Mother-in-Law.

However, it is important to note that this example is purely theoretical. In practice, Euclidean distances in high-dimensional word embeddings are not fixed but vary depending on the training data and optimization process. The relationships between words are often better captured through cosine similarity rather than absolute Euclidean distances.

Figure 7-5: Euclidean Distance.

Positional Embeddings

Since input text often contains repeated words with different meanings depending on their position, an LLM must distinguish between them. To achieve this, the word embedding process in Natural Language Processing (NLP) incorporates a Positional Encoding Vector alongside the Word Embedding Vector, resulting in the final word representation.

In Figure 7-6, the sentence "The sky is clear, so she finally decided to clear the backyard" contains the word clear twice. Repeated words share the same token ID instead of receiving unique ones. In this example, the is assigned token ID 2, and clear is assigned 5. These token IDs are then mapped to vectors using a word embedding lookup table. However, without positional encoding, words with different meanings would share the same vector representation.

Focusing on clear (token ID 5), it maps to the word embedding vector [+2.5, +1.0] from the lookup table. Since token IDs do not capture word position, identical words always receive the same embedding.

Positional encoding is essential for capturing context and semantic meaning. As shown in Figure 7-6, each input word receives a Positional Encoding Vector (PE) in addition to its word embedding. PE can either be learned and adjusted during training or remain fixed. The final Word Embedding Vector is computed by combining both the Word Embedding Vector and Positional Encoding Vector.

Figure 7-6: Tokenization – Positional Embedding Vector.

Calculating the Final Word Embedding

Figure 7-2 presents the equations for computing the final word embedding by incorporating positional embeddings. There are three variables:

• Position (pos) → The word’s position in the sentence. In our example, the first occurrence of clear is the fourth word, so pos = 4.
• Dimension (d) → The depth of the vector. We use a 2-dimensional vector, so d = 2.
• Index (i) → Specifies the axis of the vector: 0 for the x-axis and 1 for the y-axis.

The positional embedding is computed using the following equations:

• x-axis: sin(pos/100002i/d), where i = 0
• y-axis: cos(pos/100002i/d, where i = 1

For clear at position 4, with d = 2, the resulting 2D positional vector is [-0.8, +1.0]. This vector is then added to the input word embedding vector [+2.5, +1.0], resulting in the final word embedding vector [+1.7, +2.0].

Figure 7-7 also shows the final word embedding for the second occurrence of clear, but the computation is omitted.

Figure 7-7: Finals Word Embedding for the 4th Word.